Depth First Search (DFS) Algorithm

Depth first search (DFS) algorithm starts with the initial node of the graph G, and then goes to deeper and deeper until we find the goal node or the node which has no children. The algorithm, then backtracks from the dead end towards the most recent node that is yet to be completely unexplored.

The data structure which is being used in DFS is stack. The process is similar to BFS algorithm. In DFS, the edges that leads to an unvisited node are called discovery edges while the edges that leads to an already visited node are called block edges.

Algorithm

• Step 1: SET STATUS = 1 (ready state) for each node in G
• Step 2: Push the starting node A on the stack and set its STATUS = 2 (waiting state)
• Step 3: Repeat Steps 4 and 5 until STACK is empty
• Step 4: Pop the top node N. Process it and set its STATUS = 3 (processed state)
• Step 5: Push on the stack all the neighbours of N that are in the ready state (whose STATUS = 1) and set their
  STATUS = 2 (waiting state)
  [END OF LOOP]
• Step 6: EXIT

Example :

Consider the graph G along with its adjacency list, given in the figure below. Calculate the order to print all the nodes of the graph starting from node H, by using depth first search (DFS) algorithm.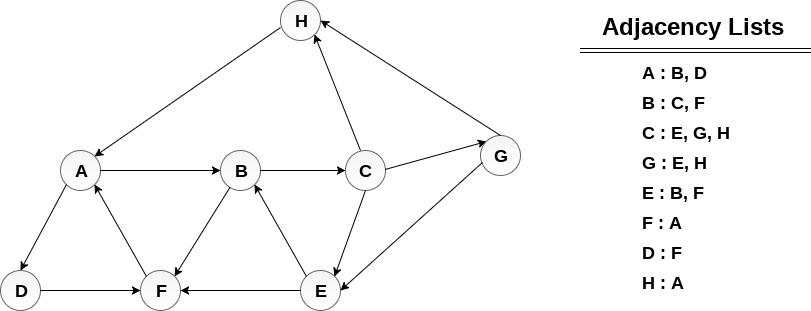

Solution :

Push H onto the stack

STACK : H 

POP the top element of the stack i.e. H, print it and push all the neighbours of H onto the stack that are is ready state.

Print H 
STACK : A 

Pop the top element of the stack i.e. A, print it and push all the neighbours of A onto the stack that are in ready state.

Print A
Stack : B, D

Pop the top element of the stack i.e. D, print it and push all the neighbours of D onto the stack that are in ready state.

Print D 
Stack : B, F 

Pop the top element of the stack i.e. F, print it and push all the neighbours of F onto the stack that are in ready state.

Print F
Stack : B

Pop the top of the stack i.e. B and push all the neighbours

Print B 
Stack : C 

Pop the top of the stack i.e. C and push all the neighbours.

Print C 
Stack : E, G 

Pop the top of the stack i.e. G and push all its neighbours.

Print G
Stack : E

Pop the top of the stack i.e. E and push all its neighbours.

Print E
Stack :

Hence, the stack now becomes empty and all the nodes of the graph have been traversed.

The printing sequence of the graph will be :

H → A → D → F → B → C → G → E