Binary Search Tree

Binary Search Tree with Introduction, Asymptotic Analysis, Array, Pointer, Structure, Singly Linked List, Doubly Linked List, Circular Linked List, Binary Search, Linear Search, Sorting, Bucket Sort, Comb Sort, Shell Sort, Heap Sort, Merge Sort, Selection Sort, Counting Sort, Stack, Qene, Circular Quene, Graph, Tree, B Tree, B+ Tree, Avl Tree etc.

<< Back to BINARY

next → ← prev

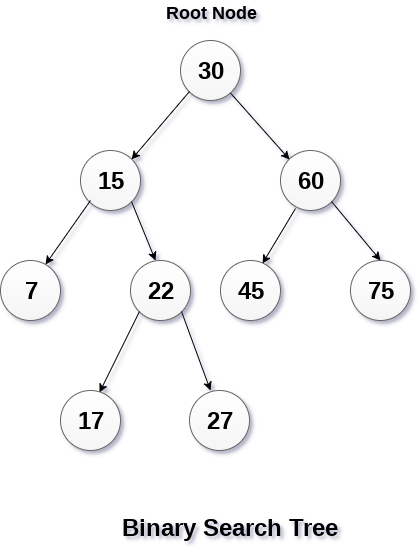
Binary Search Tree

Binary Search tree can be defined as a class of binary trees, in which the nodes are arranged in a specific order. This is also called ordered binary tree.
In a binary search tree, the value of all the nodes in the left sub-tree is less than the value of the root.
Similarly, value of all the nodes in the right sub-tree is greater than or equal to the value of the root.
This rule will be recursively applied to all the left and right sub-trees of the root.

A Binary search tree is shown in the above figure. As the constraint applied on the BST, we can see that the root node 30 doesn't contain any value greater than or equal to 30 in its left sub-tree and it also doesn't contain any value less than 30 in its right sub-tree.

Advantages of using binary search tree

Searching become very efficient in a binary search tree since, we get a hint at each step, about which sub-tree contains the desired element.
The binary search tree is considered as efficient data structure in compare to arrays and linked lists. In searching process, it removes half sub-tree at every step. Searching for an element in a binary search tree takes o(log₂n) time. In worst case, the time it takes to search an element is 0(n).
It also speed up the insertion and deletion operations as compare to that in array and linked list.

Q. Create the binary search tree using the following data elements.

43, 10, 79, 90, 12, 54, 11, 9, 50

Insert 43 into the tree as the root of the tree.
Read the next element, if it is lesser than the root node element, insert it as the root of the left sub-tree.
Otherwise, insert it as the root of the right of the right sub-tree.

The process of creating BST by using the given elements, is shown in the image below.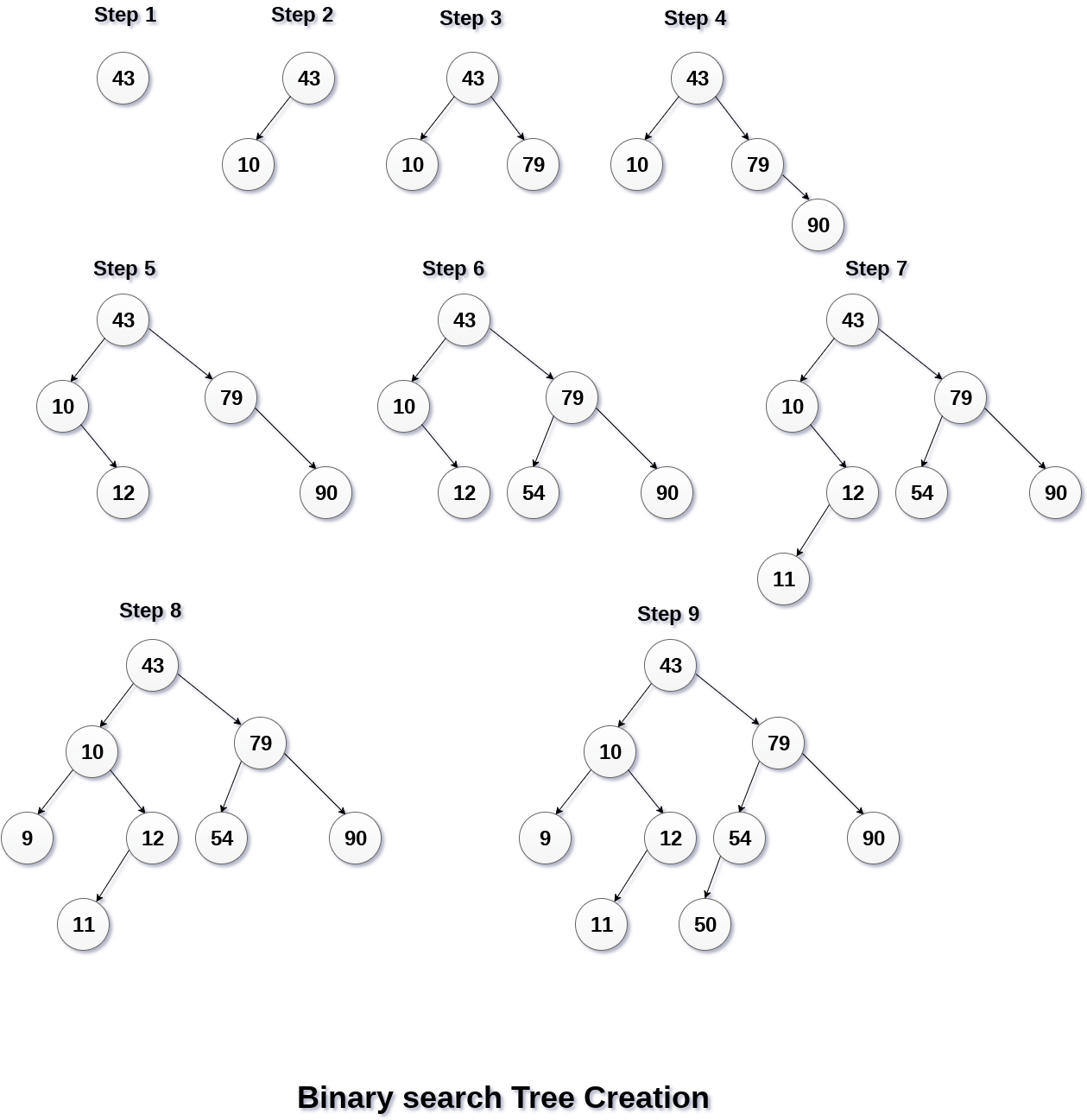

Operations on Binary Search Tree

There are many operations which can be performed on a binary search tree.

SN	Operation	Description
1	Searching in BST	Finding the location of some specific element in a binary search tree.
2	Insertion in BST	Adding a new element to the binary search tree at the appropriate location so that the property of BST do not violate.
3	Deletion in BST	Deleting some specific node from a binary search tree. However, there can be various cases in deletion depending upon the number of children, the node have.

Program to implement BST operations

#include <iostream>
#include <stdlib.h>
using namespace std;
struct Node {
    int data;
    Node *left;
    Node *right;
};
Node* create(int item)
{
    Node* node = new Node;
    node->data = item;
    node->left = node->right = NULL;
    return node;
}

void inorder(Node *root)
{
    if (root == NULL)
        return;

    inorder(root->left);
    cout<< root->data << "	";
    inorder(root->right);
}
Node* findMinimum(Node* cur)
{
    while(cur->left != NULL) {
        cur = cur->left;
    }
    return cur;
}
Node* insertion(Node* root, int item)
{
    if (root == NULL)
        return create(item);
    if (item < root->data)
        root->left = insertion(root->left, item);
    else
        root->right = insertion(root->right, item);

    return root;
}

void search(Node* &cur, int item, Node* &parent)
{
    while (cur != NULL && cur->data != item)
    {
        parent = cur;

        if (item < cur->data)
            cur = cur->left;
        else
            cur = cur->right;
    }
}

void deletion(Node*& root, int item)
{
    Node* parent = NULL;
    Node* cur = root;

    search(cur, item, parent);
    if (cur == NULL)
        return;

    if (cur->left == NULL && cur->right == NULL)
    {
        if (cur != root)
        {
            if (parent->left == cur)
                parent->left = NULL;
            else
                parent->right = NULL;
        }
        else
            root = NULL;

        free(cur);     
    }
    else if (cur->left && cur->right)
    {
        Node* succ  = findMinimum(cur- >right);

        int val = succ->data;

        deletion(root, succ->data);

        cur->data = val;
    }

    else
    {
        Node* child = (cur->left)? Cur- >left: cur->right;

        if (cur != root)
        {
            if (cur == parent->left)
                parent->left = child;
            else
                parent->right = child;
        }

        else
            root = child;
        free(cur);
    }
}

int main()
{
   Node* root = NULL;
   int keys[8];
   for(int i=0;i<8;i++)
	{
	cout << "Enter value to be inserted";
	cin>>keys[i];
        root = insertion(root, keys[i]);
	}

    inorder(root);
    cout<<"\n";
    deletion(root, 10);
    inorder(root);
    return 0;
}

Output:

Enter value to be inserted? 10
Enter value to be inserted? 20
Enter value to be inserted? 30
Enter value to be inserted? 40
Enter value to be inserted?  5 
Enter value to be inserted? 25
Enter value to be inserted? 15
Enter value to be inserted?  5

5	5	10	15	20	25	30	40	
5	5	15	20	25	30	40

Next TopicAVL Tree

← prev next →

.Net

.NET Array Dictionary List String 2D Async DataTable Dates DateTime Enum File For Foreach Format IEnumerable If IndexOf Lambda LINQ Parse Path Process Property Regex Replace Sort Split Static StringBuilder Substring Switch Tuple

Java

Core Array ArrayList HashMap String 2D Cast Character Console Deque Duplicates File For Format HashSet If IndexOf Lambda Math ParseInt Process Random Regex Replace Sort Split StringBuilder Substring Switch Vector While

TheDeveloperBlog.com

Binary Search Tree

Binary Search Tree

Advantages of using binary search tree

Q. Create the binary search tree using the following data elements.

Operations on Binary Search Tree

Program to implement BST operations

Related Links:

.Net

Java

Related Links