Deletion

Delete function is used to delete the specified node from a binary search tree. However, we must delete a node from a binary search tree in such a way, that the property of binary search tree doesn't violate. There are three situations of deleting a node from binary search tree.

The node to be deleted is a leaf node

It is the simplest case, in this case, replace the leaf node with the NULL and simple free the allocated space.

In the following image, we are deleting the node 85, since the node is a leaf node, therefore the node will be replaced with NULL and allocated space will be freed.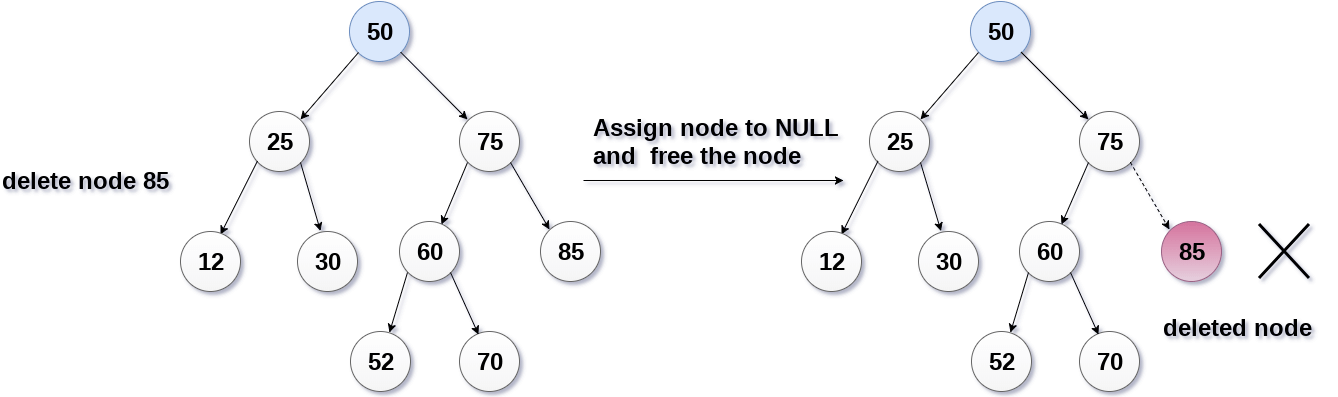

The node to be deleted has only one child.

In this case, replace the node with its child and delete the child node, which now contains the value which is to be deleted. Simply replace it with the NULL and free the allocated space.

In the following image, the node 12 is to be deleted. It has only one child. The node will be replaced with its child node and the replaced node 12 (which is now leaf node) will simply be deleted.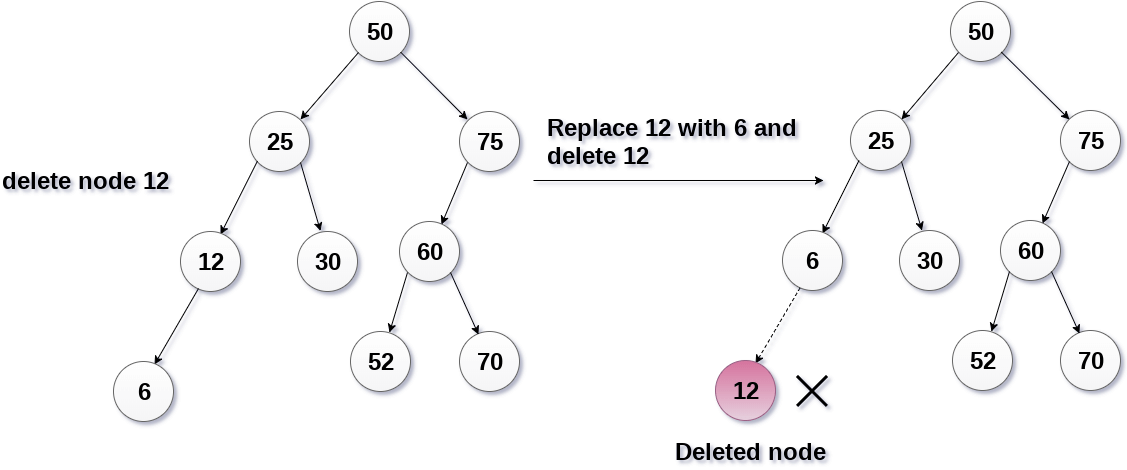

The node to be deleted has two children.

It is a bit complexed case compare to other two cases. However, the node which is to be deleted, is replaced with its in-order successor or predecessor recursively until the node value (to be deleted) is placed on the leaf of the tree. After the procedure, replace the node with NULL and free the allocated space.

In the following image, the node 50 is to be deleted which is the root node of the tree. The in-order traversal of the tree given below.

6, 25, 30, 50, 52, 60, 70, 75.

replace 50 with its in-order successor 52. Now, 50 will be moved to the leaf of the tree, which will simply be deleted.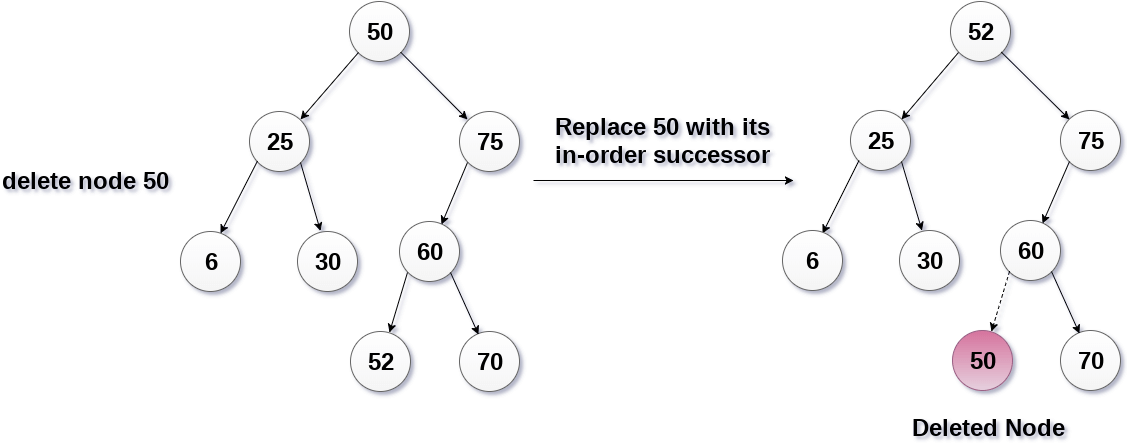

Algorithm

Delete (TREE, ITEM)

• Step 1: IF TREE = NULL
     Write "item not found in the tree" ELSE IF ITEM < TREE -> DATA
    Delete(TREE->LEFT, ITEM)
    ELSE IF ITEM > TREE -> DATA
     Delete(TREE -> RIGHT, ITEM)
    ELSE IF TREE -> LEFT AND TREE -> RIGHT
    SET TEMP = findLargestNode(TREE -> LEFT)
    SET TREE -> DATA = TEMP -> DATA
     Delete(TREE -> LEFT, TEMP -> DATA)
    ELSE
     SET TEMP = TREE
     IF TREE -> LEFT = NULL AND TREE -> RIGHT = NULL
     SET TREE = NULL
    ELSE IF TREE -> LEFT != NULL
    SET TREE = TREE -> LEFT
    ELSE
      SET TREE = TREE -> RIGHT
    [END OF IF]
    FREE TEMP
  [END OF IF]
• Step 2: END

Function:

void deletion(Node*& root, int item)
{
    Node* parent = NULL;
    Node* cur = root;

    search(cur, item, parent);
    if (cur == NULL)
        return;

    if (cur->left == NULL && cur->right == NULL)
    {
        if (cur != root)
        {
            if (parent->left == cur)
                parent->left = NULL;
            else
                parent->right = NULL;
        }
        else
            root = NULL;

        free(cur);     
    }
    else if (cur->left && cur->right)
    {
        Node* succ  = findMinimum(cur- >right);

        int val = succ->data;

        deletion(root, succ->data);

        cur->data = val;
    }

    else
    {
        Node* child = (cur->left)? Cur- >left: cur->right;

        if (cur != root)
        {
            if (cur == parent->left)
                parent->left = child;
            else
                parent->right = child;
        }

        else
            root = child;
        free(cur);
    }
}

Node* findMinimum(Node* cur)
{
    while(cur->left != NULL) {
        cur = cur->left;
    }
    return cur;
}